The Lagrange points are the five positions in an orbital configuration where a small object can remain stationary relative to two much larger bodies, interacting only via gravity.  Examples include an artificial satellite relative to the Earth–Moon system, or to the Earth–Sun system.

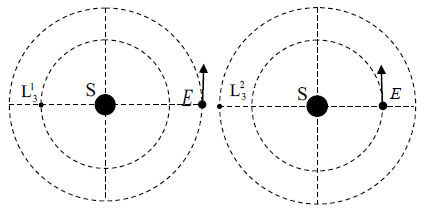
In the figure are sketched two possible orbits of Earth relative to Sun and of a small satellite relative to the Sun. At the $L_3$ point, the gravitational forces and the centrifugal force must balance. Find out which of the two points $L^1_3$ and $L^2_3$ could be the real Lagrange point relative to the system Earth – Sun, and calculate its position relative to Sun (in km).

$$d_{ES} = 15\times10^7 \rm{km} \qquad M_{Sun}/M_{Earth} = 332946$$